Giải tích và phương pháp vét cạn trong huấn luyện dữ liệu - MyGPT

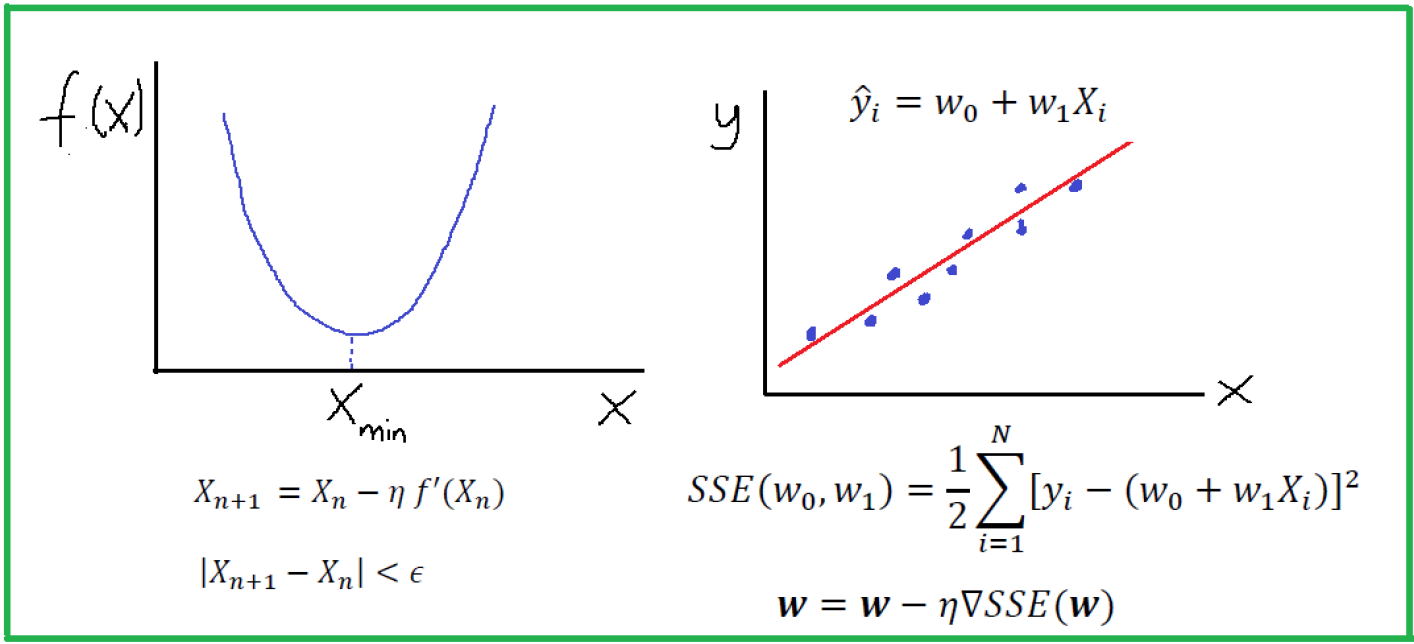
Từ hàng nghìn năm trước đây, người Hy lạp cổ đại đã tìm ra phương pháp tính diện tích hình tròn bằng cách chia nhỏ các đa giác nội tiếp thành các tam giác sau đó tính tổng diện tích các tam giác tìm được đến khi nào lượng tam giác xấp xỉ tiến tới diện tích hình tròn. Quá trình này được gọi là phương pháp vét cạn trong việc tính diện tích hình tròn.

Phương pháp vét cạn chính là khởi nguồn của Giải tích tích phân và nhánh của nó là Giải tích vi phân được áp dụng trong các bài toán tối ưu hoá để tìm ra một cách tốt nhất khi thực hiện một công việc nào đó, đặc biệt vô cùng phổ biến trong học sâu (deep learning) trên các mô hình máy tính ngày nay.

Đối với việc huấn luyện các mô hình ngôn ngữ, chúng ta sẽ áp dụng phương pháp này bằng cách cập nhật liên tục các dữ liệu liên quan đến bối cảnh để giúp cho máy ngày càng hiểu một cách tốt hơn đối với vấn đề mà chúng ta cần huấn luyện.

Thông thường, việc trở nên tốt hơn tương đương với cực tiểu hoá một hàm mất mát, một điểm số sẽ trả lời câu hỏi “mô hình của ta đang tệ tới mức nào?” Câu hỏi này lắt léo hơn ta tưởng nhiều. Mục đích cuối cùng mà ta muốn là mô hình sẽ hoạt động tốt trên dữ liệu mà nó chưa từng nhìn thấy. Nhưng chúng ta chỉ có thể khớp mô hình trên dữ liệu mà ta đang có thể thấy. Do đó ta có thể chia việc huấn luyện mô hình thành hai vấn đề chính:

• i) tối ưu hoá: quy trình huấn luyện mô hình trên dữ liệu đã thấy.
• ii) tổng quát hoá: dựa trên các nguyên tắc toán học và sự uyên thâm của người huấn luyện để tạo ra các mô hình mà tính hiệu quả của nó vượt ra khỏi tập dữ liệu huấn luyện.

Để giúp bạn hiểu rõ hơn bài toán tối ưu và các phương pháp tối ưu, trong phạm vi bài viết này chúng tôi sẽ cung cấp một số khái niệm cơ bản về các kỹ thuật giải tích vi phân thông dụng được áp dụng trong việc học sâu từ dữ liệu huấn luyện mà chúng ta hướng tới.

Đạo hàm và Vi phân

Chúng ta bắt đầu bằng việc đề cập tới khái niệm đạo hàm, một bước quan trọng của hầu hết các thuật toán tối ưu trong học sâu. Trong học sâu, ta thường chọn những hàm mất mát khả vi theo các tham số của mô hình. Nói đơn giản, với mỗi tham số, ta có thể xác định hàm mất mát tăng hoặc giảm nhanh như thế nào khi tham số đó tăng hoặc giảm chỉ một lượng cực nhỏ.

Giả sử ta có một hàm f : R→R có đầu vào và đầu ra đều là số vô hướng. Đạo hàm của f được định nghĩa như sau:

\(f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h) – f(x)}{h}, \) nếu giới hạn này tồn tại

Nếu f′(a) tồn tại, f được gọi là khả vi (differentiable) tại a. Nếu f khả vi tại mọi điểm trong một khoảng, thì hàm này được gọi là khả vi trong khoảng đó. Ta có thể giải nghĩa đạo hàm f′(x) như là tốc độ thay đổi tức thời của hàm f theo biến x. Cái gọi là tốc độ thay đổi tức thời được dựa trên độ biến thiên h trong x khi h tiến về 0.

Để minh họa cho khái niệm đạo hàm, hãy thử với một ví dụ. Định nghĩa u=f(x)=3x²−4x

%matplotlib inline
from d2l import mxnet as d2l
from IPython import display
from mxnet import np, npx
npx.set_np()

def f(x):
    return 3 * x ** 2 - 4 * x

Cho x=1 và h tiến về 0, kết quả của phương trình \(\frac{f(x+h) – f(x)}{h}\) trong công thức sẽ tiến về 2. Dù thử nghiệm này không phải là một dạng chứng minh toán học, lát nữa ta sẽ thấy rằng quả thật đạo hàm của u′ là 2 khi x=1.

def numerical_lim(f, x, h):
    return (f(x + h) - f(x)) / h

h = 0.1
for i in range(5):
    print('h=%.5f, numerical limit=%.5f' % (h, numerical_lim(f, 1, h)))
    h *= 0.1

h=0.10000, numerical limit=2.30000
h=0.01000, numerical limit=2.03000
h=0.00100, numerical limit=2.00300
h=0.00010, numerical limit=2.00030
h=0.00001, numerical limit=2.00003

Hãy làm quen với một vài ký hiệu cùng được dùng để biểu diễn đạo hàm. Cho y=f(x) với x và y lần lượt là biến độc lập và biến phụ thuộc của hàm f. Những biểu diễn sau đây là tương đương nhau:

\(f'(x) = y’ = \frac{dy}{dx} = \frac{df}{dx} = \frac{d}{dx} f(x) = Df(x) = D_x f(x),\)

với ký hiệu \(\frac{d}{dx}\) và D là các toán tử vi phân (differentiation operator) để chỉ các phép toán vi phân. Ta có thể sử dụng các quy tắc lấy đạo hàm của các hàm thông dụng sau đây:

• DC=0 (C là một hằng số),
• Dxⁿ=nxⁿ⁻¹ (quy tắc lũy thừa, n là số thực bất kỳ),
• De^x=e^x,
• Dln(x)=1/x.

Để lấy đạo hàm của một hàm được tạo từ vài hàm đơn giản hơn, ví dụ như từ những hàm thông dụng ở trên, có thể dùng các quy tắc hữu dụng dưới đây. Giả sử hàm f và g đều khả vi và C là một hằng số, ta có quy tắc nhân hằng số

\(\frac{d}{dx} [Cf(x)] = C \frac{d}{dx} f(x),\)

quy tắc tổng

\(\frac{d}{dx} [f(x) + g(x)] = \frac{d}{dx} f(x) + \frac{d}{dx} g(x),\)

quy tắc phân

\(\frac{d}{dx} [f(x)g(x)] = f(x) \frac{d}{dx} [g(x)] + g(x) \frac{d}{dx} [f(x)],\)

quy tắc đạo hàm phân thức

\(\frac{d}{dx} \left[\frac{f(x)}{g(x)}\right] = \frac{g(x) \frac{d}{dx} [f(x)] – f(x) \frac{d}{dx} [g(x)]}{[g(x)]^2}.\)

Bây giờ ta có thể áp dụng các quy tắc ở trên để tìm đạo hàm \(u’ = f'(x) = 3 \frac{d}{dx} x^2-4\frac{d}{dx}x = 6x-4\). Vậy nên, với x=1, ta có u′=2: điều này đã được kiểm chứng với thử nghiệm lúc trước ở mục này khi kết quả có được cũng tiến tới 2. Giá trị đạo hàm này cũng đồng thời là độ dốc của đường tiếp tuyến với đường cong u=f(x) tại x=1.

Để minh họa cách hiểu này của đạo hàm, ta sẽ dùng matplotlib, một thư viện vẽ biểu đồ thông dụng trong Python. Ta cần định nghĩa một số hàm để cấu hình thuộc tính của các biểu đồ được tạo ra bởi matplotlib. Trong đoạn mã sau, hàm use_svg_display chỉ định matplotlib tạo các biểu đồ ở dạng svg để có được chất lượng ảnh sắc nét hơn.

# Saved in the d2l package for later use
def use_svg_display():
    """Use the svg format to display a plot in Jupyter."""
    display.set_matplotlib_formats('svg')

Ta định nghĩa hàm set_figsize để chỉ định kích thước của biểu đồ. Lưu ý rằng ở đây ta đang dùng trực tiếp d2l.plt do câu lệnh from matplotlib import pyplot as plt đã được đánh dấu để lưu vào gói d2l trong phần Lời nói đầu.

# Saved in the d2l package for later use
def set_figsize(figsize=(3.5, 2.5)):
    """Set the figure size for matplotlib."""
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize

Ta định nghĩa hàm set_figsize để chỉ định kích thước của biểu đồ. Lưu ý rằng ở đây ta đang dùng trực tiếp d2l.plt do câu lệnh from matplotlib import pyplot as plt đã được đánh dấu để lưu vào gói d2l

# Saved in the d2l package for later use
def set_figsize(figsize=(3.5, 2.5)):
    """Set the figure size for matplotlib."""
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize

Hàm set_axes sau cấu hình thuộc tính của các trục biểu đồ tạo bởi matplotlib.

# Saved in the d2l package for later use
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    """Set the axes for matplotlib."""
    axes.set_xlabel(xlabel)
    axes.set_ylabel(ylabel)
    axes.set_xscale(xscale)
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)
    axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)
    axes.grid()

Với ba hàm cấu hình biểu đồ trên, ta định nghĩa hàm plot để vẽ nhiều đồ thị một cách nhanh chóng.

# Saved in the d2l package for later use
def plot(X, Y=None, xlabel=None, ylabel=None, legend=[], xlim=None,
         ylim=None, xscale='linear', yscale='linear',
         fmts=['-', 'm--', 'g-.', 'r:'], figsize=(3.5, 2.5), axes=None):
    """Plot data points."""
    d2l.set_figsize(figsize)
    axes = axes if axes else d2l.plt.gca()

    # Return True if X (ndarray or list) has 1 axis
    def has_one_axis(X):
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
                and not hasattr(X[0], "__len__"))

    if has_one_axis(X):
        X = [X]
    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)
    axes.cla()
    for x, y, fmt in zip(X, Y, fmts):
        if len(x):
            axes.plot(x, y, fmt)
        else:
            axes.plot(y, fmt)
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)

Giờ ta có thể vẽ đồ thị của hàm số u=f(x) và đường tiếp tuyến của nó y=2x−3 tại x=1, với hệ số 2 là độ dốc của tiếp tuyến.

x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

Đạo hàm riêng

Như đề cập ở trên, chúng ta đã làm việc với đạo hàm một biến, tuy nhiên trong học sâu với dữ liệu thì nó luôn tồn tại nhiều biến do đó chúng ta cần mở rộng mô phỏng này với đạo hàm nhiều biến số dưới dạng như sau:

Cho y=f(x1,x2,…,xn) là một hàm với n biến số. Và Đạo hàm riêng của y theo tham số thứ i và biến x_i (x tại i) là:

\(\frac{\partial y}{\partial x_i} = \lim_{h \rightarrow 0} \frac{f(x_1, \ldots, x_{i-1}, x_i+h, x_{i+1}, \ldots, x_n) – f(x_1, \ldots, x_i, \ldots, x_n)}{h}.\)

Để tính \(\frac{\partial y}{\partial x_i}\) ta chỉ cần coi x₁,…,x_i-1,x_i+1,…,x_n là hằng số và tính đạo hàm của y theo x_i và để biểu diễn đạo hàm riêng, các ký hiệu sau đây đều có ý nghĩa tương đương:

\(\frac{\partial y}{\partial x_i} = \frac{\partial f}{\partial x_i} = f_{x_i} = f_i = D_i f = D_{x_i} f.\)

Gradient

Chúng ta có thể ghép các đạo hàm riêng của mọi biến trong một hàm nhiều biến để thu được vector gradient của hàm số đó. Giả sử rằng đầu vào của hàm \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) là một vector n chiều \(\mathbf{x} = [x_1, x_2, \ldots, x_n]^\top\) và đầu ra là một số vô hướng. Gradient của hàm f(x) theo x là một vector gồm n đạo hàm riêng đó:

\(\nabla_{\mathbf{x}} f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_n}\bigg]^\top.\)

Biểu thức ∇_xf(x) thường được viết gọn thành ∇f(x) trong trường hợp không sợ nhầm lẫn.

Cho x là một vector n chiều, các quy tắc sau thường được dùng khi tính vi phân hàm đa biến:

• Với mọi A∈R^m×n, ∇_xAx=A^⊤,
• Với mọi A∈R^n×m, ∇_xx^⊤A=A,
• Với mọi A∈R^n×n, ∇_xx^⊤Ax=(A+A^⊤),
• ∇_x∥x∥²=∇_xx^⊤x=2x.

Tương tự, với bất kỳ ma trận X nào, ta đều có \(\nabla_{\mathbf{X}} \|\mathbf{X} \|_F^2 = 2\mathbf{X}\). Sau này ta sẽ thấy, gradient sẽ rất hữu ích khi thiết kế thuật toán tối ưu trong học sâu.

Quy tắc dây chuyền

Các vector gradient có thể khó tính toán để lấy vi phân do đa phần các hàm nhiều biến trong học sâu thường là những hàm hợp tuy nhiên có một quy tắc khác giúp ta có thể lấy vi phân các hàm hợp này đó là quy tắc dây chuyền.

Trước tiên, chúng ta hãy xem xét các hàm một biến. Giả sử hai hàm y=f(u) và u=g(x) đều khả vi, quy tắc dây chuyền được mô tả như sau

\(\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}.\)

Giờ ta sẽ xét trường hợp tổng quát hơn đối với các hàm nhiều biến. Giả sử một hàm khả vi y có các biến số u₁,u₂,…,u_m trong đó mỗi biến u_i là một hàm khả vi của các biến x₁,x₂,…,x_n. Lưu ý rằng y cũng là hàm của các biến x₁,x₂,…,x_n. Quy tắc dây chuyền cho ta

\(\frac{dy}{dx_i} = \frac{dy}{du_1} \frac{du_1}{dx_i} + \frac{dy}{du_2} \frac{du_2}{dx_i} + \cdots + \frac{dy}{du_m} \frac{du_m}{dx_i}\)

cho mỗi i=1,2,…,n

Kết luận

• Vi phân, tích phân là hai nhánh con của bộ môn Giải tích trong đó vi phân được ứng dụng trong bài toán tối ưu hoá của học sâu nhằm vét cạn các miền biểu diễn dữ liệu được mô phỏng trên máy.
• Đạo hàm có thể được hiểu như là tốc độ thay đổi tức thì của một hàm số đối với các biến số. Nó cũng là độ dốc của đường tiếp tuyến với đường cong của hàm.
• Gradient là một vector có các phần tử là đạo hàm riêng của một hàm nhiều biến theo tất cả các biến số của nó.
• Quy tắc dây chuyền cho phép chúng ta lấy vi phân của các hàm hợp.

Hiểu được các cách thức tổ chức cũng như ứng dụng toán học giải tích vào các bài toán trong học sâu sẽ giúp cho chúng ta có thể mô hình hoá và mường tượng được về mặt phương pháp tổ chức dữ liệu thực tế cũng như cách thức hiệu chỉnh, sắp xếp dữ liệu trong quá trình turning phù hợp nhằm mang lại hiệu quả tốt nhất khi huấn luyện dữ liệu tại các miền dùng riêng trên thực tế.

Lời cảm ơn

myGPT team cảm ơn các dịch giả có tên dưới đây

• Đoàn Võ Duy Thanh
• Lê Khắc Hồng Phúc
• Phạm Hồng Vinh
• Vũ Hữu Tiệp
• Nguyễn Cảnh Thướng
• Phạm Minh Đức
• Tạ H. Duy Nguyên

đã thực hiện biên dịch cuốn Dive into Deep Learning, dựa vào các nội dung này, chúng tôi diễn giải lại cho sát với thực tế của việc huấn luyện dữ liệu giúp cho người dùng cũng như các thành viên trong nhóm xử lý dữ liệu có thể có được một phương pháp xử lý và tổ chức tốt hơn.